Context

OpenGL is a popular graphics programming specification that is supported by most GPUs used today. It is implemented via graphics drivers that are typically written in C and provided by the GPU manufacturer, along with client and API libraries, typically written in assembly, C or C++, the latter of which a programmer can use to interact with the GPU. PyOpenGL is a Python binding to the OpenGL API, which is implemented with Python's ctypes foreign function interface and bridges the gap between Python and the lower-level API library, providing a close replica of the OpenGL API in Python.

This article provides a basic overview of the OpenGL API, before detailing the mathematical transformations required to render a 3D cube to a 2D display. This theory is demonstrated via an implementation of the classic rotating cube exercise in PyOpenGL, without heavy reliance on GLM, which is OpenGL's mathematics library. This library abstracts the underlying maths by providing a set of functions for constructing transformation matrices, but we will instead implement these transformations ourselves.

OpenGL Overview

The OpenGL API operates like a state machine which we can interact with in one of two ways: by calling a function which changes the state (e.g., linking a new shader program) or by calling a function which performs an action using the current state (e.g., drawing a shape to the screen). This state is called the OpenGL context and is organised like a C struct, where different sub-components (called objects) can be swapped in and out (called binding and unbinding respectively).

The transformation of 3D objects in memory to 2D pixels on a screen is performed by OpenGL's graphics pipeline, comprised of a sequence of programs called shaders which run on the GPU and are written in GLSL (which stands for "openGL Shading Language"). Modern GPUs have hundreds or even thousands of cores, each capable of running a shader in parallel, which is why GPUs are so much faster than CPUs for graphics processing (modern CPUs typically have 4-8 far more generalised cores).

The first stage of the graphics pipeline is the vertex shader, for which there is no default (we must provide our own implementation of this step). This shader receives a single vertex as input, whose 3D coordinates $(x,y,z) \in \mathbb{R}^3$ are in "local space", meaning they are relative to the origin of the object the vertex belongs to. This shader is responsible for converting these local coordinates into 3D homogeneous "clip space" coordinates $(x_C, y_C, z_C, w_C) \in \mathbb{R}^4$, which are then used to determine which parts of objects are visible on the screen. The vertex shader also forwards any other data associated with the vertex for use in later stages of the pipeline (such as 2D texture coordinates). This local to clip space conversion is achieved by applying a sequence of transformations:

  1. the model transformation converts local coordinates to world coordinates, using information about the object's position, orientation and size in the world we are rendering, and hence is the combination of a scale, translation and rotation transformation;
  2. the view transformation converts world coordinates to view/camera coordinates, using information about the position and orientation of the camera in the world, and hence is the combination of a translation and rotation transformation; and
  3. the projection transformation converts camera coordinates to clip space coordinates, using information about the camera's type (orthographic or perspective), field of view, aspect ratio and range.

Following the vertex shader in the graphics pipeline (ignoring some advanced, optional steps) is the primitive assembly stage, where a set of processed vertices are grouped into a sequence of primitives (points, lines or triangles, depending on the context). Next is the clipping stage, where primitives lying outside the viewing volume (defined by $-w_C \le x_C \le w_C$ and likewise for $y_C$ and $z_C$) are discarded, and primitives only partially inside the volume are clipped to fit within it (a triangle may be split into multiple triangles here). Next is the perspective divide into normalised device coordinates: $$ (x_{\text{NDC}}, y_{\text{NDC}}, z_{\text{NDC}}) \> = \> (\frac{x_C}{w_C}, \frac{y_C}{w_C}, \frac{z_C}{w_C}) \> \in \> [-1,1]^3. $$ After this is the viewport transformation, which converts NDC to window coordinates, which depends on the window size in pixels and the size of the device's depth buffer. Next is face culling, where triangle primitives facing away from view in window space can be discarded, such that they don't need to be rendered. Then the pipeline performs rasterisation, where each primitive is mapped to a set of fragments, with at least one fragment per pixel displaying the primitive. A fragment is a collection of all data required to render a single pixel to the screen (which includes data that was forwarded from the vertex shader).

The next stage is the fragment shader, which, like the vertex shader, has no default implementation. This shader receives a single fragment as input and returns a colour to be drawn to the screen at its corresponding pixel (as well as some other data including depth). The final stage of the graphics pipeline is a sequence of "per-sample" operations on each fragment, which include pixel ownership testing (which fails if the fragment's pixel location is owned by another overlapping window), depth testing (checking if this fragment is behind another fragment and should be discarded) and blending (combining the fragment's colour with a colour already in the frame buffer for this pixel, to handle opacity).

Transformation Matrices

We now have a basic, theoretical understanding of how OpenGL works. However, before we can move on to writing any PyOpenGL code, we need to understand what a transformation matrix is and derive the matrix representations of scale, translation and rotation transformations. Using these, we will define the model, view and projection transformations required by our vertex shader.

Given a vertex with coordinates $(x,y,z) \in \mathbb{R}^3$, we represent this point in space by the vector of homogeneous coordinates $$\begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} \in \mathbb{R}^4,$$ where the fourth coordinate will remain 1 until the projection transformation. Given this definition, we can represent a transformation of this point by a real, 4x4 matrix that is left-multiplied by the vector. An affine transformation such as a scaling, translation or rotation can be achieved with a matrix multiplication of the form $$ \begin{pmatrix} a_{11} & a_{12} & a_{13} & b_1 \\ a_{21} & a_{22} & a_{23} & b_2 \\ a_{31} & a_{32} & a_{33} & b_3 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} \> = \> \begin{pmatrix} a_{11} x + a_{12} y + a_{13} z + b_1 \\ a_{21} x + a_{22} y + a_{23} z + b_2 \\ a_{31} x + a_{32} y + a_{33} z + b_3 \\ 1 \end{pmatrix}, $$ and hence combining transformations (e.g., a rotation followed by a translation) is equivalent to multiplying their representative matrices. The inclusion of the fourth coordinate may seem pointless, but it allows us to represent translation and perspective projection transformations as matrix multiplications, which would not be possible with 3x3 matrices.

A scale transformation with scaling factors $s_X, s_Y$ and $s_Z$ converts a point $(x,y,z,1)$ to the point $(s_X x, s_Y y, s_Z z, 1)$, which is achieved by multiplying by the diagonal matrix $$\begin{pmatrix} s_X & 0 & 0 & 0 \\ 0 & s_Y & 0 & 0 \\ 0 & 0 & s_Z & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}.$$ We can write a Python function which returns this matrix as a 2D NumPy array given a set of scaling factors. 

import numpy as np
import numpy.typing as npt


def scale_matrix(s_x: float, s_y: float, s_z: float) -> npt.NDArray:
    assert s_x > 0 and s_y > 0 and s_z > 0, "Input factors must be positive"
    return np.array([
        [s_x, 0.0, 0.0, 0.0],
        [0.0, s_y, 0.0, 0.0],
        [0.0, 0.0, s_z, 0.0],
        [0.0, 0.0, 0.0, 1.0]
    ])

A translation transformation which translates by distance $t_X$ in the $x$-direction, $t_Y$ in the $y$-direction and $t_Z$ in the $z$-direction, thus converting a point $(x,y,z,1)$ to the point $(x + t_X, y + t_Y, z + t_Z, 1)$, is achieved by the matrix $$\begin{pmatrix} 1 & 0 & 0 & t_X \\ 0 & 1 & 0 & t_Y \\ 0 & 0 & 1 & t_Z \\ 0 & 0 & 0 & 1 \end{pmatrix}.$$ This transformation can also be implemented as a simple Python function. 

def translation_matrix(t_x: float, t_y: float, t_z: float) -> npt.NDArray:
    return np.array([
        [1.0, 0.0, 0.0, t_x],
        [0.0, 1.0, 0.0, t_y],
        [0.0, 0.0, 1.0, t_z],
        [0.0, 0.0, 0.0, 1.0]
    ])

A rotation in 3D space is defined by a (unit vector) axis and an angle of rotation about that axis. Any rotation in three dimensions can be achieved by a composition of rotations about the standard basis vectors $$ \boldsymbol{i} = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}, \>\> \boldsymbol{j} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}, \>\> \boldsymbol{k} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}. $$ Let's focus on a rotation about the $z$-axis / basis vector $\boldsymbol{k}$ by some acute angle $\theta \in (0,\frac{\pi}{2})$ radians, and consider how the other two basis vectors $\boldsymbol{i}$ and $\boldsymbol{j}$ are transformed to vectors $\boldsymbol{i}^{\prime}$ and $\boldsymbol{j}^{\prime}$ respectively.

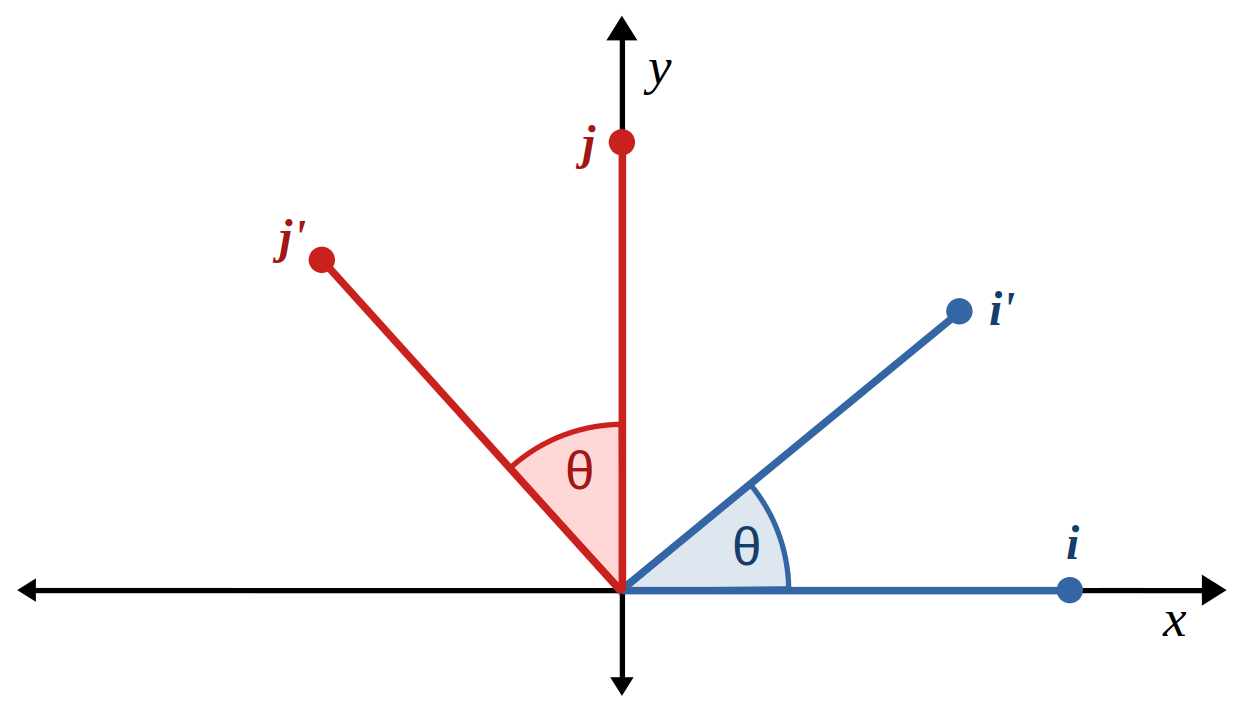
Diagram of 3D standard basis vectors i and j rotated about k.

We can form a right-angled triangle in the first quadrant of the $xy$-plane with $\boldsymbol{i}^{\prime}$ as the hypotenuse, its $x$-component the adjacent side and its $y$-component the opposite side. The hypotenuse has unit length because a rotation preserves the length of a vector, and the angle at the origin is $\theta$, and hence the definitions of sine and cosine give $$ \cos(\theta) = \frac{\text{adj}}{\text{hyp}} = \frac{i^{\prime}_x}{1}, \>\> \sin(\theta) = \frac{\text{opp}}{\text{hyp}} = \frac{i^{\prime}_y}{1}, $$ and of course $i^{\prime}_z = 0$ because $i_z = 0$. Forming a similar right-angled triangle between $\boldsymbol{j}^{\prime}$ and its components (noting that $j^{\prime}_x < 0$), we find that $$ \cos(\theta) = \frac{j^{\prime}_y}{1}, \>\> \sin(\theta) = \frac{-j^{\prime}_x}{1}, $$ and $j^{\prime}_z = 0$. Therefore we have that the acute rotation transforms the standard basis vectors to $$ \boldsymbol{i}^{\prime} = \begin{pmatrix} \cos(\theta) \\ \sin(\theta) \\ 0 \end{pmatrix}, \>\> \boldsymbol{j}^{\prime} = \begin{pmatrix} -\sin(\theta) \\ \cos(\theta) \\ 0 \end{pmatrix}, \>\> \boldsymbol{k}^{\prime} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}. $$ It can be shown that these results generalise to a rotation by any angle $\theta$. For an obtuse $\theta$, we can draw the above triangles for the acute angle $180^{\circ} - \theta$ between the rotated basis vector and the $x$ and $y$ axes, then using the fact that $\cos(180^{\circ}-\theta) = -\cos(\theta)$ and $\sin(180^{\circ}-\theta) = \sin(\theta)$, we will arrive at the same transformed basis vectors. A similar approach can be used for reflex angles $\theta$, then utilising the fact that angles that are equal modulo $360^{\circ}$ produce equivalent rotations, we can claim that the above results apply to any angle $\theta$.

For a general vector $\boldsymbol{v}$, the definition of the standard basis vectors gives us that $$ \boldsymbol{v} \> = \> \begin{pmatrix} v_x \\ v_y \\ v_z \end{pmatrix} \> = \> v_x \boldsymbol{i} + v_y \boldsymbol{j} + v_z \boldsymbol{k} $$ (i.e., $\boldsymbol{v}$ is a linear combination of the standard basis vectors, with coefficients equal to its entries), and hence the rotation of $\boldsymbol{v}$ about the $z$-axis by angle $\theta$ is $$ \boldsymbol{v}^{\prime} \> = \> v_x \boldsymbol{i}^{\prime} + v_y \boldsymbol{j}^{\prime} + v_z \boldsymbol{k}^{\prime} \> = \> \begin{pmatrix} \cos(\theta)v_x - \sin(\theta)v_y \\ \sin(\theta)v_x + \cos(\theta)v_y \\ v_z \end{pmatrix} $$ because affine transformations (of which a rotation is an example) preserve linear combinations of vectors. Finally, returning to 3D homogeneous coordinates, we can equate this transformation to multiplication by the matrix $$\begin{pmatrix} \cos \theta & -\sin \theta & 0 & 0 \\ \sin \theta & \cos \theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}.$$ An equivalent derivation can be performed for a rotation about the $x$-axis by an angle $\theta$ to find that its matrix is $$\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos \theta & -\sin \theta & 0 \\ 0 & \sin \theta & \cos \theta & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix},$$ and similarly, a rotation about the $y$-axis by $\theta$ is represented by the matrix $$\begin{pmatrix} \cos \theta & 0 & \sin \theta & 0 \\ 0 & 1 & 0 & 0 \\ -\sin \theta & 0 & \cos \theta & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}.$$ We won't derive this nor use it in our implementation, but for the sake of completeness, a rotation about an arbitrary unit vector axis $(r_X,r_Y,r_Z)$ by an angle $\theta$ is represented by the matrix $$ \begin{pmatrix} \cos \theta + r_X^2 (1 - \cos \theta) & r_X r_Y (1 - \cos \theta) - r_Z \sin \theta & r_X r_Z (1 - \cos \theta) + r_Y \sin \theta & 0 \\ r_Y r_X (1 - \cos \theta) + r_Z \sin \theta & \cos \theta + r_Y^2 (1 - \cos \theta) & r_Y r_Z (1 - \cos \theta) - r_X \sin \theta & 0 \\ r_Z r_X (1 - \cos \theta) - r_Y \sin \theta & r_Z r_Y (1 - \cos \theta) + r_X \sin \theta & \cos \theta + r_Z^2 (1 - \cos \theta) & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}, $$ which, as mentioned already, can also be achieved by a product of the three basis vector rotations (but this approach can sometimes lead to numerical instability, so many advanced programs using vector rotations prefer to use a direct rotation like this). Given angles of rotation about the $x$, $y$ and $z$ axes, we can write a Python function which returns the resulting rotation matrix product, with flexible input parameters that allow the angles to be provided in degrees or radians. 

def rotation_matrix(
    theta_x_deg: float = 0.0,
    theta_x_rad: float = 0.0,
    theta_y_deg: float = 0.0,
    theta_y_rad: float = 0.0,
    theta_z_deg: float = 0.0,
    theta_z_rad: float = 0.0
) -> npt.NDArray:
    # convert inputs to radians
    assert (theta_x_deg == 0.0) or (theta_x_rad == 0.0), (
        "Either provide theta_x in degrees or radians, not both"
    )
    if theta_x_deg != 0.0:
        theta_x_rad = theta_x_deg * np.pi / 180.0

    assert (theta_y_deg == 0.0) or (theta_y_rad == 0.0), (
        "Either provide theta_y in degrees or radians, not both"
    )
    if theta_y_deg != 0.0:
        theta_y_rad = theta_y_deg * np.pi / 180.0

    assert (theta_z_deg == 0.0) or (theta_z_rad == 0.0), (
        "Either provide theta_z in degrees or radians, not both"
    )
    if theta_z_deg != 0.0:
        theta_z_rad = theta_z_deg * np.pi / 180.0

    # init identity matrix to handle no rotation
    rot_matrix = np.array([
        [1.0, 0.0, 0.0, 0.0],
        [0.0, 1.0, 0.0, 0.0],
        [0.0, 0.0, 1.0, 0.0],
        [0.0, 0.0, 0.0, 1.0]
    ])

    if theta_x_rad != 0.0:
        sin = np.sin(theta_x_rad)
        cos = np.cos(theta_x_rad)
        rot_matrix @= np.array([
            [1.0, 0.0, 0.0, 0.0],
            [0.0, cos, -sin, 0.0],
            [0.0, sin, cos, 0.0],
            [0.0, 0.0, 0.0, 1.0]
        ])
    if theta_y_rad != 0.0:
        sin = np.sin(theta_y_rad)
        cos = np.cos(theta_y_rad)
        rot_matrix @= np.array([
            [cos, 0.0, sin, 0.0],
            [0.0, 1.0, 0.0, 0.0],
            [-sin, 0.0, cos, 0.0],
            [0.0, 0.0, 0.0, 1.0]
        ])
    if theta_z_rad != 0.0:
        sin = np.sin(theta_z_rad)
        cos = np.cos(theta_z_rad)
        rot_matrix @= np.array([
            [cos, -sin, 0.0, 0.0],
            [sin, cos, 0.0, 0.0],
            [0.0, 0.0, 1.0, 0.0],
            [0.0, 0.0, 0.0, 1.0]
        ])

    return rot_matrix

Model and View Transformations

We have derived the matrix representations of scale, translation and rotation transformations, and written some handy Python functions which construct these matrices as 2D Numpy arrays. We can now use these to write utility functions which, given the appropriate parameters, return matrices for the model and view transformations.

The model transformation in the vertex shader transforms a vertex's local coordinates to world coordinates, using the position, orientation and scale of the object that the vertex belongs to. Hence, the model transformation matrix is the product of a scale, rotation and translation matrix (in that order, as scaling after translating would also scale the translation). Therefore, we can construct a model matrix by calling our scale, rotation and translation functions and multiplying these component matrices together in the correct order. 

def model_matrix(
    scale_x: float = 1.0,
    scale_y: float = 1.0,
    scale_z: float = 1.0,
    rot_x_deg: float = 0.0,
    rot_x_rad: float = 0.0,
    rot_y_deg: float = 0.0,
    rot_y_rad: float = 0.0,
    rot_z_deg: float = 0.0,
    rot_z_rad: float = 0.0,
    trans_x: float = 0.0,
    trans_y: float = 0.0,
    trans_z: float = 0.0
) -> npt.NDArray:
    model = scale_matrix(scale_x, scale_y, scale_z)
    if (
        rot_x_deg != 0.0 or rot_x_rad != 0.0 or
        rot_y_deg != 0.0 or rot_y_rad != 0.0 or
        rot_z_deg != 0.0 or rot_z_rad != 0.0
    ):
        model @= rotation_matrix(rot_x_deg, rot_x_rad, rot_y_deg, rot_y_rad, rot_z_deg, rot_z_rad)
    if trans_x != 0.0 or trans_y != 0.0 or trans_z != 0.0:
        model @= translation_matrix(trans_x, trans_y, trans_z)
    return model

The view transformation in the vertex shader transforms a vertex's world coordinates to view coordinates, using the position and orientation of the camera in the world, in order to render the world from the camera's perspective. Hence, the view transformation matrix is the product of a translation and rotation matrix (in that order, as the rotation axis should stem from the camera's position). Note that the first three arguments of the function below specify the position of the camera in the world, and hence the translation required to "move" the camera to the origin uses the negation of these coordinates. 

def view_matrix(
    camera_x: float = 0.0,
    camera_y: float = 0.0,
    camera_z: float = 0.0,
    rot_x_deg: float = 0.0,
    rot_x_rad: float = 0.0,
    rot_y_deg: float = 0.0,
    rot_y_rad: float = 0.0,
    rot_z_deg: float = 0.0,
    rot_z_rad: float = 0.0
) -> npt.NDArray:
    view = translation_matrix(-camera_x, -camera_y, -camera_z)
    if (
        rot_x_deg != 0.0 or rot_x_rad != 0.0 or
        rot_y_deg != 0.0 or rot_y_rad != 0.0 or
        rot_z_deg != 0.0 or rot_z_rad != 0.0
    ):
        view @= rotation_matrix(rot_x_deg, rot_x_rad, rot_y_deg, rot_y_rad, rot_z_deg, rot_z_rad)
    return view

Projection Transformation

The final transformation required by the vertex shader is the projection transformation. For this article, we will focus on just the perspective projection, which results in a "realistic" rendering of a 3D scene, as opposed to an orthographic projection which results in a "flat" rendering (which is useful for some applications such as CAD software). The perspective projection transformation defines a "rectangular frustum" volume in camera space which is indirectly transformed to the $[-1,1]$ cube in NDC/viewport space. This frustum is a sideways pyramid with a rectangle for a base and its apex cut off (with the base facing away from the camera and the clipped apex pointing towards the camera). We say "indirectly", because this matrix actually transforms from camera space to "clip space" (which still uses 3D homogeneous coordinates), which is a precursor to NDC space. After the vertex shader, OpenGL efficiently performs the perspective divide to convert clip space coordinates to NDC, which completes the transformation from the frustum to the cube.

The inputs defining this transformation are:

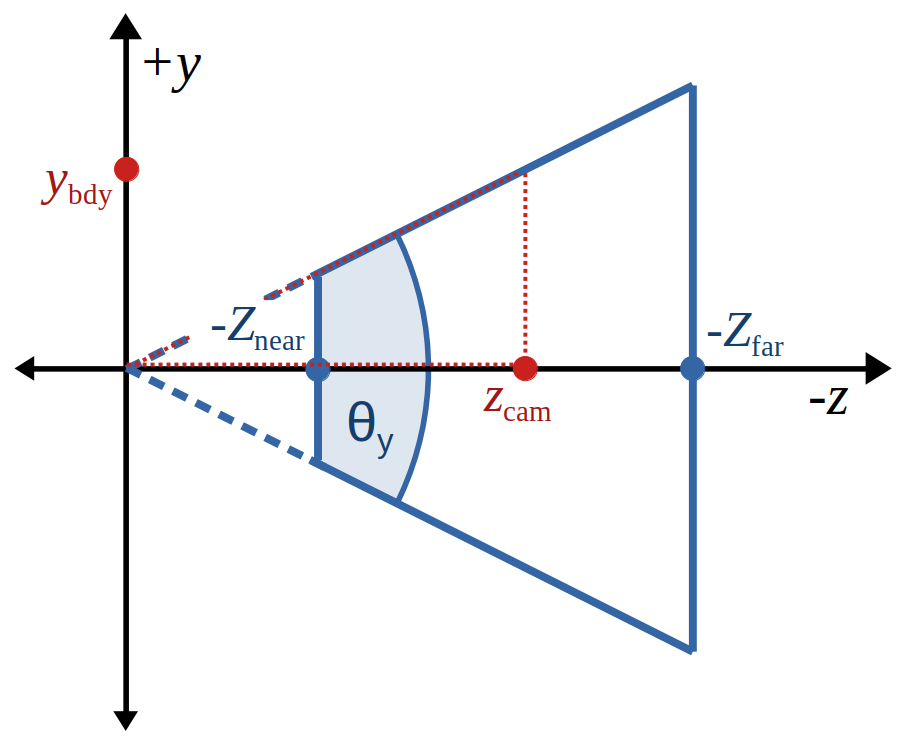
Diagram of rectangular frustum in camera space.

To derive the perspective projection matrix, let's forget about clip space for a moment and instead consider the whole transformation from camera space to NDC (i.e., from the frustum to the $[-1,1]$ cube). We will denote camera space coordinates by $x_{\text{cam}}$, $y_{\text{cam}}$ and $z_{\text{cam}}$, and NDC coordinates by $x_{\text{NDC}}$, $y_{\text{NDC}}$ and $z_{\text{NDC}}$.

Given some $z_{\text{cam}} \in [-Z_{\text{far}}, -Z_{\text{near}}]$ inside the frustum, we can draw a right-angled triangle on the $zy$-plane between the points $(0,0,0)$, $(0,0,z_{\text{cam}})$ and $(0,y_{\text{bdy}},z_{\text{cam}})$, where $y_{\text{bdy}}$ is the half-height of the frustum at this $z$-coordinate (so the third point lies on the top trapezium face of the frustum). The angle inside this triangle at the origin is $\frac{\theta_y}{2}$, and hence we can claim that $$\begin{aligned} \tan\left(\frac{\theta_y}{2}\right) \> &= \> \frac{y_{\text{bdy}}}{-z_{\text{cam}}} \\ \Rightarrow \> y_{\text{bdy}} \> &= \> \tan\left(\frac{\theta_y}{2}\right) \cdot -z_{\text{cam}} \\ &= \> \frac{-z_{\text{cam}}}{F_y}, \end{aligned}$$ by defining the constant factor $$F_y \> = \> \frac{1}{\tan\left(\frac{\theta_y}{2}\right)}.$$ We have derived an expression for $y_{\text{bdy}}$, which is the half-height of the frustum at any $z_{\text{cam}}$ inside the volume. At this $z$-coordinate, the perspective projection will linearly transform $y_{\text{cam}} \in [-y_{\text{bdy}},y_{\text{bdy}}]$ to $y_{\text{NDC}} \in [-1,1]$, and hence $$\begin{aligned} y_{\text{NDC}} &= \frac{y_{\text{cam}}}{y_{\text{bdy}}} \\ &= \> y_{\text{cam}} \cdot \frac{F_y}{-z_{\text{cam}}}. \end{aligned}$$ We can apply the exact same logic to derive an expression for $x_{\text{NDC}}$, using a modified factor $$F_x \> = \> \frac{F_y}{A},$$ where dividing by the aspect ratio accounts for the different width of the frustum along the x-axis, and so $$x_{\text{NDC}} \> = \> x_{\text{cam}} \cdot \frac{F_y}{A \cdot -z_{\text{cam}}}.$$ The inclusion of $-z_{\text{cam}}$ on the denominator of the expressions for $x_{\text{NDC}}$ and $y_{\text{NDC}}$ is what causes objects further from the camera to appear smaller on the screen, which is a defining quality of the perspective projection over the orthographic projection.

Now it is left to transform $z_{\text{cam}} \in [-Z_{\text{far}}, -Z_{\text{near}}]$ to $z_{\text{NDC}} \in [-1, 1]$. The standard approach is to use a reciprocal function such that objects further from the camera appear smaller in depth, and it also ensures that $z$-coordinates closer to the camera consume a disproportionately large part of the depth buffer (because objects close to the camera will be focused on more by the viewer, and hence numerical imprecision causing objects that should have slightly different $z$-coordinates to instead overlap would be more problematic if seen up close). Therefore, we establish that $$z_{\text{NDC}} \> = \> \frac{\alpha}{z_{\text{cam}}} + \beta$$ for some constants $\alpha$ and $\beta$. We know that the near plane of the frustum $z_{\text{cam}} = -Z_{\text{near}}$ is transformed to the close face of the cube $z_{\text{NDC}} = -1$, and substituting this gives $$\begin{aligned} -1 \> &= \frac{\alpha}{-Z_{\text{near}}} + \beta \\ \Rightarrow \> -1 - \beta \> &= \frac{\alpha}{-Z_{\text{near}}} \\ \Rightarrow \> \alpha \> &= (-1 - \beta) \cdot -Z_{\text{near}}. \end{aligned}$$ Similarly, we know that the far plane of the frustum $z_{\text{cam}} = -Z_{\text{far}}$ is transformed to the far face of the cube $z_{\text{NDC}} = 1$, and so $$\begin{aligned} 1 \> &= \frac{\alpha}{-Z_{\text{far}}} + \beta \\ \Rightarrow \> 1 - \beta \> &= \frac{\alpha}{-Z_{\text{far}}} \\ \Rightarrow \> \alpha \> &= (1 - \beta) \cdot -Z_{\text{far}}. \end{aligned}$$ Equating these two expressions for $\alpha$ gives $$\begin{aligned} (-1 - \beta) \cdot -Z_{\text{near}} \> &= \> (1 - \beta) \cdot -Z_{\text{far}} \\ \Rightarrow \> Z_{\text{near}} + \beta Z_{\text{near}} \> &= \> -Z_{\text{far}} + \beta Z_{\text{far}} \\ \Rightarrow \> \beta Z_{\text{near}} - \beta Z_{\text{far}} \> &= \> -Z_{\text{far}} - Z_{\text{near}} \\ \Rightarrow \> \beta \> &= \> -\frac{Z_{\text{far}} + Z_{\text{near}}}{Z_{\text{near}} - Z_{\text{far}}}, \end{aligned}$$ which is the constant value of $\beta$. Substituting this back into the second expression for $\alpha$ shows that $$\begin{aligned} \alpha \> &= \> (1 - \beta) \cdot -Z_{\text{far}} \\ &= \> (1 + \frac{Z_{\text{far}} + Z_{\text{near}}}{Z_{\text{near}} - Z_{\text{far}}}) \cdot -Z_{\text{far}} \\ &= \> -Z_{\text{far}} \frac{Z_{\text{near}} - Z_{\text{far}} + Z_{\text{far}} + Z_{\text{near}}}{Z_{\text{near}} - Z_{\text{far}}} \\ &= \> -\frac{2 Z_{\text{near}} Z_{\text{far}}}{Z_{\text{near}} - Z_{\text{far}}}. \end{aligned}$$ Finally, substituting these constants back into our formula for $z_{\text{NDC}}$ concludes that $$\begin{aligned} z_{\text{NDC}} \> &= \> \frac{\alpha}{z_{\text{cam}}} + \beta \\ &= \> - \frac{2 Z_{\text{near}} Z_{\text{far}}}{z_{\text{cam}}(Z_{\text{near}} - Z_{\text{far}})} - \frac{Z_{\text{far}} + Z_{\text{near}}}{Z_{\text{near}} - Z_{\text{far}}} \\ &= \> \frac{-2 Z_{\text{near}} Z_{\text{far}} - z_{\text{cam}}(Z_{\text{far}} + Z_{\text{near}})} {z_{\text{cam}}(Z_{\text{near}} - Z_{\text{far}})} \\ &= \> \frac{1}{-z_{\text{cam}}} \left( \frac{Z_{\text{far}} + Z_{\text{near}}}{Z_{\text{near}} - Z_{\text{far}}} z_{\text{cam}} + \frac{2 Z_{\text{near}} Z_{\text{far}}}{Z_{\text{near}} - Z_{\text{far}}} \right). \end{aligned}$$

We have now derived equations for $x_{\text{NDC}}$, $y_{\text{NDC}}$ and $z_{\text{NDC}}$ in terms of $x_{\text{cam}}$, $y_{\text{cam}}$ and $z_{\text{cam}}$, but notice that these form a non-linear transformation from camera space to NDC/viewport space due to the common divisor of $-z_{\text{cam}}$ in the formulae. This is where the purpose of the intermediate "clip space" becomes evident. As previously defined, NDC are computed from clip space coordinates using the perspective divide operation (which OpenGL performs very efficiently for us) $$ x_{\text{NDC}} = \frac{x_{\text{clip}}}{w_{\text{clip}}}, \> y_{\text{NDC}} = \frac{y_{\text{clip}}}{w_{\text{clip}}}, \> z_{\text{NDC}} = \frac{z_{\text{clip}}}{w_{\text{clip}}}. $$ If we define $w_{\text{clip}} = -z_{\text{cam}}$, then the NDC equations we derived give us $$\begin{aligned} x_{\text{clip}} \> &= \> \frac{F_y}{A} \cdot x_{\text{cam}}, \\ y_{\text{clip}} \> &= \> F_y \cdot y_{\text{cam}}, \\ z_{\text{clip}} \> &= \> \frac{Z_{\text{far}} + Z_{\text{near}}}{Z_{\text{near}} - Z_{\text{far}}} \cdot z_{\text{cam}} + \frac{2 Z_{\text{near}} Z_{\text{far}}}{Z_{\text{near}} - Z_{\text{far}}}, \end{aligned}$$ all of which are linear equations of the camera coordinates. Therefore, we can define the perspective projection transformation from camera space to clip space as multiplication by the matrix $$\begin{pmatrix} \frac{F_y}{A} & 0 & 0 & 0 \\ 0 & F_y & 0 & 0 \\ 0 & 0 & \frac{Z_{\text{far}} + Z_{\text{near}}}{Z_{\text{near}} - Z_{\text{far}}} & \frac{2 Z_{\text{near}} Z_{\text{far}}}{Z_{\text{near}} - Z_{\text{far}}} \\ 0 & 0 & -1 & 0 \end{pmatrix}.$$ Finally, we can implement a simple Python function that returns this matrix given the field of view, aspect ratio, and the near and far clipping planes. 

def projection_matrix(
    fov_y_deg: float = 0.0,
    fov_y_rad: float = 0.0,
    aspect_ratio: float = 4/3,
    z_near: float = 0.1,
    z_far: float = 10.0
) -> npt.NDArray:
    assert aspect_ratio > 0.0, "aspect_ratio must be > 0"
    assert 0 <= z_near < z_far, "z_near must be >= 0 and z_far must be > z_near"

    # convert input to radians
    assert (fov_y_deg > 0.0) != (fov_y_rad > 0.0), "Exactly one field of view input must be provided"
    if fov_y_rad == 0.0:
        fov_y_rad = fov_y_deg * np.pi / 180.0

    factor_y = 1 / (np.tan(fov_y_rad / 2))

    return np.array([
        [factor_y / aspect_ratio, 0.0, 0.0, 0.0],
        [0.0, factor_y, 0.0, 0.0],
        [0.0, 0.0, (z_far + z_near) / (z_near - z_far), (2 * z_near * z_far) / (z_near - z_far)],
        [0.0, 0.0, -1.0, 0.0]
    ])

PyOpenGL Implementation

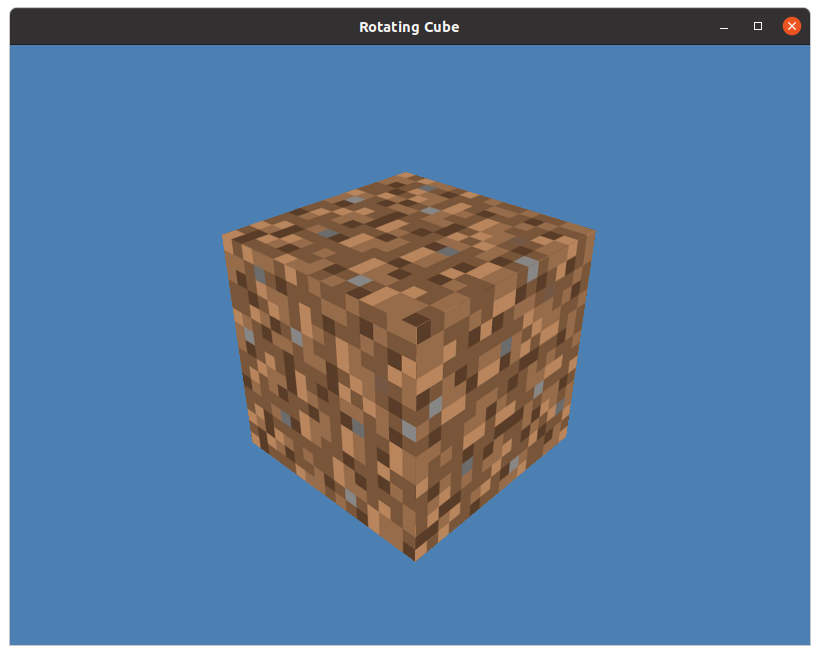
We will now put our understanding of OpenGL and the mathematics of matrix transformations to use by implementing a Python program which renders a rotating, textured cube. We will start by implementing a series of PyOpenGL utility functions (to handle core procedures such as initialising a window, compiling shaders, loading textures and sending data to the GPU), as well as defining our vertex and fragment shaders. We will then use these functions to write a succinct main program for rendering the rotating cube.

The first utility function we need to define is one that initialises a window for us to render in. We will use pyGLFW, which is a Python binding to GLFW, an OpenGL utility library that provides a simple API for managing windows and handling input. This function receives the window's title, width and height (in pixels) as input, and starts by initialising GLFW, which involves setting the OpenGL version and profile (the core profile is the most modern and doesn't include deprecated features). It then creates a window (alongside its OpenGL context, which is then made current) and sets a callback function to handle window resizing. Finally, OpenGL is configured, which in our case only involves enabling depth testing (which will ensure that closer objects are rendered in front of objects further from the camera). This function returns the window object for later use. 

import glfw
from OpenGL.GL import *


def framebuffer_size_callback(window: glfw._GLFWwindow, width: int, height: int) -> None:
    glViewport(0, 0, width, height)


def init_glfw_window_opengl(title: str, screen_width: int = 800, screen_height: int = 600) -> glfw._GLFWwindow:
    # init GLFW
    if not glfw.init():
        raise RuntimeError("Failed to initialise GLFW")

    glfw.window_hint(glfw.CONTEXT_VERSION_MAJOR, 3)
    glfw.window_hint(glfw.CONTEXT_VERSION_MINOR, 3)
    glfw.window_hint(glfw.OPENGL_PROFILE, glfw.OPENGL_CORE_PROFILE)

    # create window
    window = glfw.create_window(screen_width, screen_height, title, None, None)
    if not window:
        glfw.terminate()
        raise RuntimeError("Failed to create GLFW window")

    glfw.make_context_current(window)
    glfw.set_framebuffer_size_callback(window, framebuffer_size_callback)

    # init OpenGL options
    glEnable(GL_DEPTH_TEST)

    return window

Before we continue with PyOpenGL, we need to define our vertex and fragment shaders. We write our shaders in GLSL (the OpenGL Shading Language), which is very similar to C but also provides vector and matrix types tailored for graphics programming. The vertex shader is written as follows: 

#version 330 core
layout (location = 0) in vec3 input_pos;
layout (location = 1) in vec2 input_tex_coord;

out vec2 texture_coord;

uniform mat4 model;
uniform mat4 view;
uniform mat4 projection;

void main()
{
    gl_Position = projection * view * model * vec4(input_pos, 1.0f);
    texture_coord = vec2(input_tex_coord.x, input_tex_coord.y);
}

We save the above vertex shader code to a file called vertex_shader.vs. We also define our fragment shader and save it to a file called fragment_shader.fs, and this shader is written as follows: 

#version 330 core
in vec2 texture_coord;

out vec4 fragment_colour;

uniform sampler2D texture1;

void main()
{
    fragment_colour = texture(texture1, texture_coord);
}

Now that we have defined our shaders, we implement a utility function which loads a shader's source code from file, creates an OpenGL "shader object" for it, attaches the source code and compiles it, then returns the shader object's ID. This function also checks for compilation errors, such that this utility function successfully returning implies that the shader's source code is valid. The arguments to this function are simply the file path of the shader's source code and the type of shader (either "vertex" or "fragment"). 

from OpenGL.GL import *
from pathlib import Path


def load_shader(file_name: str, shader_type: str = "vertex") -> int:
    if not Path(file_name).exists():
        raise FileNotFoundError(f"{shader_type.capitalize()} shader file not found: {file_name}")

    with open(file_name) as f:
        shader_src = f.read()
    
    shader_id = glCreateShader(GL_VERTEX_SHADER if shader_type == "vertex" else GL_FRAGMENT_SHADER)
    glShaderSource(shader_id, shader_src)
    glCompileShader(shader_id)

    success = glGetShaderiv(shader_id, GL_COMPILE_STATUS)
    if not success:
        raise RuntimeError(f"Failed to compile {shader_type} shader: {glGetShaderInfoLog(shader_id).decode()}")

    return shader_id

After using the above function to initialise a vertex shader and fragment shader, the next step is to create a "shader program", which is an object comprising compiled shaders that are linked together (where outputs are matched to downstream inputs to check for compatibility). We can then bind this shader program to the OpenGL context to use it for rendering. This utility function receives a vertex shader ID and fragment shader ID as input, attaches them to a new shader program, links the program (checking for errors), deletes the individual shader objects, then returns the new shader program's ID. 

from OpenGL.GL import *


def create_shader_program(vertex_shader_id: int, fragment_shader_id: int) -> int:
    program_id = glCreateProgram()
    glAttachShader(program_id, vertex_shader_id)
    glAttachShader(program_id, fragment_shader_id)
    glLinkProgram(program_id)

    success = glGetProgramiv(program_id, GL_LINK_STATUS)
    if not success:
        raise RuntimeError(f"Failed to link shader program: {glGetProgramInfoLog(program_id).decode()}")

    glDeleteShader(vertex_shader_id)
    glDeleteShader(fragment_shader_id)

    return program_id

We now look to implement a utility function that loads the vertex data for a unit cube, which comprises five floating point numbers per vertex: the $x$, $y$ and $z$ coordinates of the vertex in model space, and the 2D texture coordinates $s$ and $t$. Given a 2D texture, the bottom-left corner has coordinates $(s,t) = (0,0)$ and the top-right corner has coordinates $(1,1)$. Specifying the texture coordinates for each vertex of the cube defines precisely how the texture is to be mapped onto the cube's faces, as each fragment's texture coordinate is interpolated from the vertex texture coordinates of the primitive (in our case, the triangle) it belongs to. The fragment shader performs the task of sampling from the texture at these interpolated coordinates to determine the fragment's colour.

This function begins by defining the vertices of the unit cube as a 1D GLM floating point array, where each square face is defined by two triangle primitives (each of which is defined by three vertices). Next, we create a vertex array object (VAO, which stores vertex attribute configurations) and a vertex buffer object (VBO, which stores vertex data such that it can be sent to the GPU all at once instead of one vertex at a time). We bind the VAO and VBO to the current OpenGL context, then load the vertex data into the VBO by specifying: which bound buffer to load data into, the size of the data in bytes, a pointer to the data, and a GPU usage hint (in our case, GL_STATIC_DRAW indicates that the data will not be modified frequently). Finally, we call the glVertexAttribPointer function (per vertex attribute) to specify the layout of the vertex data in the VBO:

Following each call to this function, we call glEnableVertexAttribArray to enable the attribute (all vertex attributes are disabled by default). Finally, our utility function returns the VAO and VBO IDs and the number of vertices comprising the cube. Note that we only need the VBO ID for deleting this object when the program terminates, as the VAO maintains an internal reference to the VBO which we will use when rendering. 

from OpenGL.GL import *
import glm


def vertex_array_buffer_objs_for_unit_cube() -> tuple[int, int, int]:
    vertices = glm.array(glm.float32,
        # positions        texture coords
        -0.5, -0.5, -0.5,  0.0, 0.0,
         0.5, -0.5, -0.5,  1.0, 0.0,
         0.5,  0.5, -0.5,  1.0, 1.0,
         0.5,  0.5, -0.5,  1.0, 1.0,
        -0.5,  0.5, -0.5,  0.0, 1.0,
        -0.5, -0.5, -0.5,  0.0, 0.0,

        -0.5, -0.5,  0.5,  0.0, 0.0,
         0.5, -0.5,  0.5,  1.0, 0.0,
         0.5,  0.5,  0.5,  1.0, 1.0,
         0.5,  0.5,  0.5,  1.0, 1.0,
        -0.5,  0.5,  0.5,  0.0, 1.0,
        -0.5, -0.5,  0.5,  0.0, 0.0,

        -0.5,  0.5,  0.5,  1.0, 0.0,
        -0.5,  0.5, -0.5,  1.0, 1.0,
        -0.5, -0.5, -0.5,  0.0, 1.0,
        -0.5, -0.5, -0.5,  0.0, 1.0,
        -0.5, -0.5,  0.5,  0.0, 0.0,
        -0.5,  0.5,  0.5,  1.0, 0.0,

         0.5,  0.5,  0.5,  1.0, 0.0,
         0.5,  0.5, -0.5,  1.0, 1.0,
         0.5, -0.5, -0.5,  0.0, 1.0,
         0.5, -0.5, -0.5,  0.0, 1.0,
         0.5, -0.5,  0.5,  0.0, 0.0,
         0.5,  0.5,  0.5,  1.0, 0.0,

        -0.5, -0.5, -0.5,  0.0, 1.0,
         0.5, -0.5, -0.5,  1.0, 1.0,
         0.5, -0.5,  0.5,  1.0, 0.0,
         0.5, -0.5,  0.5,  1.0, 0.0,
        -0.5, -0.5,  0.5,  0.0, 0.0,
        -0.5, -0.5, -0.5,  0.0, 1.0,

        -0.5,  0.5, -0.5,  0.0, 1.0,
         0.5,  0.5, -0.5,  1.0, 1.0,
         0.5,  0.5,  0.5,  1.0, 0.0,
         0.5,  0.5,  0.5,  1.0, 0.0,
        -0.5,  0.5,  0.5,  0.0, 0.0,
        -0.5,  0.5, -0.5,  0.0, 1.0
    )

    vao_id = glGenVertexArrays(1)
    vbo_id = glGenBuffers(1)

    glBindVertexArray(vao_id)

    glBindBuffer(GL_ARRAY_BUFFER, vbo_id)
    glBufferData(GL_ARRAY_BUFFER, vertices.nbytes, vertices.ptr, GL_STATIC_DRAW)

    # position attribute
    glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 5 * glm.sizeof(glm.float32), None)
    glEnableVertexAttribArray(0)

    # texture coord attribute
    glVertexAttribPointer(
        1, 2, GL_FLOAT, GL_FALSE, 5 * glm.sizeof(glm.float32), ctypes.c_void_p(3 * glm.sizeof(glm.float32))
    )
    glEnableVertexAttribArray(1)

    return vao_id, vbo_id, len(vertices) // 5

Next up, we need a utility function for loading a texture from an image file. This function receives the file path of the texture image as input and: 

from OpenGL.GL import *
from pathlib import Path
from PIL import Image


def load_texture(file_path: str) -> int:
    file_path = Path(file_path)
    if not file_path.exists():
        raise FileNotFoundError(f"Texture file not found: {file_path}")
    if file_path.suffix not in [".jpg", ".png"]:
        raise ValueError(f"Texture file must be a .jpg or .png file: {file_path}")

    texture_id = glGenTextures(1)
    glBindTexture(GL_TEXTURE_2D, texture_id)

    # set texture wrapping and filtering params
    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_REPEAT)
    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_REPEAT)
    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR_MIPMAP_LINEAR)
    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR)

    img = Image.open(file_path).transpose(Image.FLIP_TOP_BOTTOM)

    glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB, img.width, img.height, 0, GL_RGB, GL_UNSIGNED_BYTE, img.tobytes())
    glGenerateMipmap(GL_TEXTURE_2D)

    img.close()
    return texture_id

We have yet to handle sending uniform data to the GPU to be used by our vertex and fragment shaders. This next utility function handles sending a 4x4 matrix to the GPU, which we will use for our model, view and projection matrices. This function takes as input the shader program ID, the name of the uniform variable (as defined in the shader code) and the matrix as a Numpy array. We first check that the matrix is 4x4, then query OpenGL for the location of the uniform variable in the shader program, before assigning the matrix data to the uniform variable using the glUniformMatrix4fv function (which takes the uniform location, the number of matrices to send, a boolean indicating if the matrix should be transposed, and a pointer to the matrix data). If the uniform was not found, this function raises an exception. 

from OpenGL.GL import *
import glm
import numpy as np
import numpy.typing as npt


def send_matrix_to_shader(program_id: int, uniform_name: str, matrix: npt.NDArray[np.float32]):
    assert matrix.shape == (4, 4), f"Matrix must be 4x4, got {matrix.shape} instead"
    uniform_location = glGetUniformLocation(program_id, uniform_name)
    if uniform_location == -1:
        raise RuntimeError(f"Failed to locate uniform: {uniform_name}")
    matrix = glm.mat4(matrix)
    glUniformMatrix4fv(uniform_location, 1, GL_FALSE, glm.value_ptr(matrix))

Next up, we define a utility function that sets the "texture unit" of each sampler uniform in the shader program. Texture units allow us to use multiple textures in a shader program (even though in this application, we only use one), by assigning each sampler uniform a unique texture unit that we activate before binding a texture to it. This function takes the shader program ID and an ordered list of sampler uniform names as input. It calls glUseProgram to activate our shader program, then iterates through each uniform name, querying OpenGL for the location of the uniform in the shader program and assigning the next free texture unit (starting with 0) to it. 

from OpenGL.GL import *


def shader_program_set_sampler_texture_units(program_id: int, sampler_names: list[str]):
    glUseProgram(program_id)
    for unit, sampler_name in enumerate(sampler_names):
        glUniform1i(glGetUniformLocation(program_id, sampler_name), unit)

We now define a utility function that binds texture objects to texture units. Given an ordered list of the application's texture object IDs (ordered by texture unit as set by the previous function), for each texture unit, this function activates the texture unit and then calls glBindTexture with the corresponding texture object ID, which binds that texture object to the texture unit, which will allow the fragment shader to sample the texture from that texture unit's uniform sampler. 

from OpenGL.GL import *


def bind_textures_to_texture_units(texture_ids: list[int]):
    assert len(texture_ids) <= 16, "Only up to 16 texture units are supported"
    for unit, texture_id in enumerate(texture_ids):
        glActiveTexture(GL_TEXTURE0 + unit)
        glBindTexture(GL_TEXTURE_2D, texture_id)

In this tutorial we will handle only a single user input: the escape key. To do this, we define a process_input function which is called at the beginning of the main rendering loop. We use GLFW's get_key function to check if the escape key is currently being pressed, and if it is, we set GLFW's window_should_close flag to True, which will cause the main loop to exit before the next iteration. 

import glfw


def process_input(window: glfw._GLFWwindow) -> None:
    if glfw.get_key(window, glfw.KEY_ESCAPE) == glfw.PRESS:
        glfw.set_window_should_close(window, True)

This next utility function clears the screen with a background colour and activates our shader program, and should be called immediately after the above process_input function in the main rendering loop. It receives the shader program ID and the background colour as input, calls glClearColor to set the background colour, which is then used when glClear is called. We tell OpenGL to clear both the colour and depth buffers (such that any trace of the previous frame is removed), Finally, we activate our shader program, as following this function, the main program will be setting uniforms and drawing geometry. 

from OpenGL.GL import *


def clear_screen_before_render(
    program_id: int, background_colour: tuple[float, float, float, float]
):
    glClearColor(*background_colour)
    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
    glUseProgram(program_id)

We have already defined functions to set uniforms for matrices and texture units, so it remains to implement a function that actually renders the unit cube. This function takes the VAO ID and the number of vertices as input, and starts by binding the VAO to the current OpenGL context. We then call glDrawArrays which, using the currently active shader program, the previously configured vertex attributes and the vertex data in the VBO (which was indirectly bound by binding the VAO), draws the cube's triangles to the screen. We simply pass the primitive type GL_TRIANGLES, the initial vertex index (0) and the number of vertices to draw. 

from OpenGL.GL import *


def render_triangles(vao_id: int, num_vertices: int):
    glBindVertexArray(vao_id)
    glDrawArrays(GL_TRIANGLES, 0, num_vertices)

The final utility function we will implement is one that runs after the main loop has exited, but before the program terminates. this function is responsible for deleting the vertex array and buffer objects that we created for the unit cube, before terminating the GLFW library. 

import glfw
from OpenGL.GL import *


def terminate(vao_id: int, vbo_id: int):
    glDeleteVertexArrays(1, (vao_id,))
    glDeleteBuffers(1, (vbo_id,))
    glfw.terminate()

Finally, we can put all of these utility functions to use in our main program, which will render a rotating, textured cube. This main program has two main sections: the first of these is the initialisation section, where we set up the window, shader program, vertex array and buffer objects (as well as our vertex attribute configuration), and our texture with its texture unit. The other section is the main rendering loop, where we process user input, clear the screen, bind the texture to its texture unit, define the model, view and projection matrices, send these to the GPU via their respective uniforms, and finally render the cube.

Following the rendering, we call GLFW's swap_buffers function. To understand what this does, we first need to understand that OpenGL uses "double buffering": the front colour buffer (a large 2D buffer storing the colour of each pixel in the window) contains the image currently being displayed, whilst our rendering commands write to the back buffer. After we are finished rendering, calling swap_buffers swaps the back buffer to the front buffer which displays the new image in an instant. If OpenGL used a single buffer for rendering, the user might see intermediate rendering steps, flickering or artifacts on the screen. We also call poll_events which checks for input events (keyboard or mouse), which we then handle at the beginning of the next iteration of the main loop. This loop is terminated when GLFW's window_should_close function returns True, which we control in the process_input function when the escape key is pressed. Finally, we call our terminate utility function to clean up some of our OpenGL objects before actually terminating the program. 

import glfw
from utils import *


SCREEN_TITLE = "Rotating Cube"
SCREEN_WIDTH_PX = 800
SCREEN_HEIGHT_PX = 600


window = init_glfw_window_opengl(
    title=SCREEN_TITLE, screen_width=SCREEN_WIDTH_PX, screen_height=SCREEN_HEIGHT_PX
)

vertex_shader_id = load_shader(file_name="vertex_shader.vs", shader_type="vertex")
fragment_shader_id = load_shader(file_name="fragment_shader.fs", shader_type="fragment")
shader_program_id = create_shader_program(vertex_shader_id, fragment_shader_id)

vao_id, vbo_id, num_vertices = vertex_array_buffer_objs_for_unit_cube()

texture_id = load_texture("texture.jpg")
shader_program_set_sampler_texture_units(shader_program_id, sampler_names=["texture1"])


# main rendering loop
while not glfw.window_should_close(window):
    process_input(window)

    clear_screen_before_render(
        shader_program_id, background_colour=(0.3, 0.5, 0.7, 1.0)
    )

    bind_textures_to_texture_units(texture_ids=[texture_id])

    model = model_matrix(
        rot_x_rad=0.67 * glfw.get_time(),
        rot_y_rad=glfw.get_time()
    )
    send_matrix_to_shader(shader_program_id, "model", model)

    view = view_matrix(camera_x=0.0, camera_y=0.0, camera_z=-3.0)
    send_matrix_to_shader(shader_program_id, "view", view)

    projection = projection_matrix(
        fov_y_deg=45.0,
        aspect_ratio=SCREEN_WIDTH_PX / SCREEN_HEIGHT_PX,
        z_near=0.1,
        z_far=100.0
    )
    send_matrix_to_shader(shader_program_id, "projection", projection)

    render_triangles(vao_id, num_vertices)

    glfw.swap_buffers(window)
    glfw.poll_events()

terminate(vao_id, vbo_id)

Running the Program

To run this demonstration on a Linux machine, you will need to create a directory containing the following files:

You will also need install the latest versions of the following pip packages into a Python environment: numpy, PyOpenGL, PyGLM, glfw and pillow. To run the program, simply execute python3 main.py after activating your Python environment, and you will see a new window open displaying a rotating, textured cube.

Window created by running this program which displays a rotating cube.

References

  1. de Vries, Joey. "OpenGL." Learn OpenGL, 2014, learnopengl.com/Getting-started/OpenGL.
  2. "Rendering Pipeline Overview." OpenGL Wiki, 2022, www.khronos.org/opengl/wiki/Rendering_Pipeline_Overview .
  3. Morlan, Austin. "Deriving the 3D Rotation Matrix." Austinmorlan.com, 20 Apr. 2021, austinmorlan.com/posts/rotation_matrices/.
  4. Giuca, Matt. "Calculating the GluPerspective Matrix and Other OpenGL Matrix Maths." Unspecified Behaviour, 21 June 2012, unspecified.wordpress.com/2012/06/21/calculating-the-gluperspective-matrix-and-other-opengl-matrix-maths/ .

If you have any corrections or questions - please send me an email and we can have a discussion. Any edits or additions to the original article & code will be noted here.